The variation principle
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص381-383َ
2025-11-29
35
The variation principle
A more systematic way of discussing bond polarity and finding the coefficients in the linear combinations used to build molecular orbitals is provided by the variation principle: If an arbitrary wavefunction is used to calculate the energy, the value calculated is never less than the true energy. This principle is the basis of all modern molecular structure calculations (Section 11.7). The arbitrary wavِefunction is called the trial wavefunction. The principle implies that, if we vary the coefficients in the trial wavefunction until the lowest energy is achieved (by evaluating the expectation value of the hamiltonian for each wavefunction), then those coefficients will be the best. We might get a lower energy if we use a more complicated wavefuncِtion (for example, by taking a linear combination of several atomic orbitals on each atom), but we shall have the optimum (minimum energy) molecular orbital that can be built from the chosen basis set, the given set of atomic orbitals.
The method can be illustrated by the trial wavefunction in eqn 11.21. We show in the Justification below that the coefficients are given by the solutions of the two secular equations
(αA −E) cA+(β−ES) cB=0
(β −ES) cA +(αB−E) cB=0
The parameter α is called a Coulomb integral. It is negative and can be interpreted as the energy of the electron when it occupies A (for αA) or B (for αB). In a homo nuclear diatomic molecule, αA = αB. The parameter β is called a resonance integral (for classical reasons). It vanishes when the orbitals do not overlap, and at equilibrium bond lengths it is normally negative.
Justification 11.3 The variation principle applied to a heteronuclear diatomic molecule The trial wavefunction in eqn 11.21 is real but not normalized because at this stage the coefficients can take arbitrary values. Therefore, we can write ψ* = ψ but do not assume that ∫ψ2dτ = 1. The energy of the trial wavefunction is the expectation value of the energy operator (the hamiltonian, H, Section 8.5):
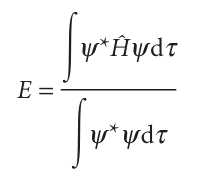
We must search for values of the coefficients in the trial function that minimize the value of E. This is a standard problem in calculus, and is solved by finding the coefficients for which
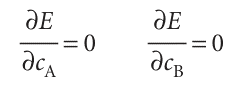
The first step is to express the two integrals in terms of the coefficients. The denominator is
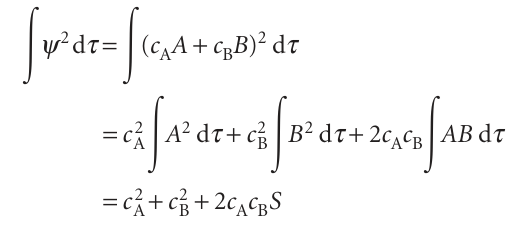
because the individual atomic orbitals are normalized and the third integral is the overlap integral S (eqn 11.17). The numerator is
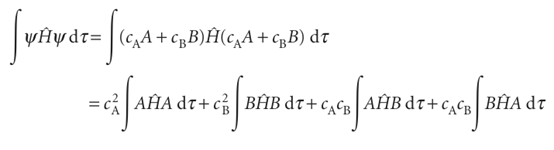
There are some complicated integrals in this expression, but we can combine them all into the parameters
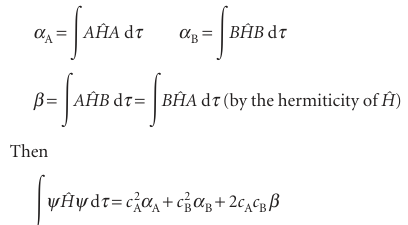
The complete expression for E is
Its minimum is found by differentiation with respect to the two coefficients and set ting the results equal to 0. After a bit of work, we obtain
For the derivatives to vanish, the numerators of the expressions above must vanish. That is, we must find values of Ca and cB that satisfy the conditions
AαA−cAE+cBβ−cBSE=(αA−E)cA+(β−ES)cB=0 cAβ−cASE+cBαB−cBE=(β−ES)cA+(αB−E)cB=0
To solve the secular equations for the coefficients we need to know the energy E of the orbital. As for any set of simultaneous equations, the secular equations have a solution if the secular determinant, the determinant of the coefficients, is zero; that is, if
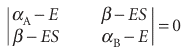
This determinant expands to a quadratic equation in E(see Illustration 11.2). Its two roots give the energies of the bonding and antibonding molecular orbitals formed from the atomic orbitals and, according to the variation principle, the lower root is the best energy achievable with the given basis set.
The values of the coefficients in the linear combination are obtained by solving the secular equations using the two energies obtained from the secular determinant. The lower energy (E+in the Illustration) gives the coefficients for the bonding molecular orbital, the upper energy (E−) the coefficients for the antibonding molecular orbital. The secular equations give expressions for the ratio of the coefficients in each case, so we need a further equation in order to find their individual values. This equation is obtained by demanding that the best wavefunction should also be normalized. This condition means that, at this final stage, we must also ensure that
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
